Two Pointers & Prefix Sum
Two pointers and Prefix sum are two algorithm solving techniques. In this post, I dissect their differences from their similarities.
Two pointers and Prefix sum are two algorithm solving techniques. In this post, I dissect their differences from their similarities.
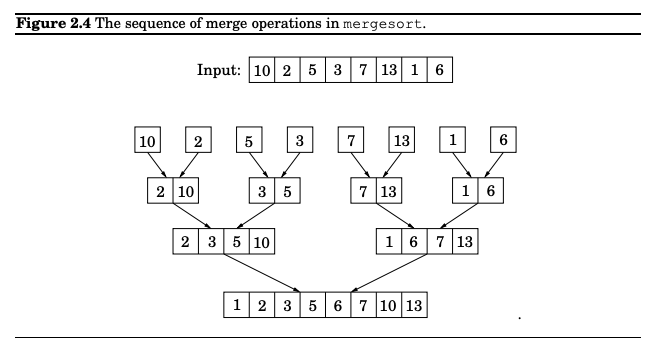
As a divide and conquer algorithm, in this article, we look deeply into merge sort, simplifying its core concepts with a binary search algorithm.
Going through Chapter 2 of CLRS, I was introduced to the concept of divide and conquer, which is a very interesting algorithm technique, and a popular example of the divide and conquer algorithm is merge sort. Merge sort has an Θ(nlgn) run time, which is very good for large inputs. When the input is sufficiently small enough, the algorithm has a worse run time compared to a sorting algorithm that completes in Θ(n^2) time. One of the exercises is to create an optimized version of the merge sort that runs the original merge sort algorithm for sufficiently larger inputs where it shines and to run insertion sort [ Θ(n^2) ] when the input size is sufficiently small enough. I have a solution for it on my Clio website, this post walks through the process for the solution. ...
Solution to Exercise 1.1-1 Question
Solution to Exercise 1.1-2 Question
Solution to Exercise 1.1-3 Question
Solution to Exercise 1.1-4 Question
Solution to Exercise 1.1-5 Question
Solution to Exercise 1.1-6 Question
Solution to Problem 1.1-1